Ученые разгадали научную загадку, которая будоражила человеческие умы практически 140 лет!

Математики доказали, что четырехчастное разбиение Генри Дьюдени 1907 года равностороннего треугольника на квадрат является оптимальным. Используя диаграммы соответствия, исследователи из JAIST и MIT показали, что трехчастного решения не существует, что стало первым формальным доказательством оптимальности в задачах разбиения. Их работа нашла применение в математике, инженерии и материаловедении.

В 1907 году английский писатель и математик Генри Эрнест Дьюдени сформулировал увлекательную головоломку: можно ли разрезать равносторонний треугольник на наименьшее количество частей, которые можно переставить так, чтобы получился идеальный квадрат? Всего четыре недели спустя он представил элегантное решение, показав, что для этого нужно всего четыре части. Этот метод разрезания фигуры на части и перестановки их для формирования другой фигуры известен как рассечение. Центральной задачей при рассечении является минимизация количества частей, необходимых для преобразования одного многоугольника в другой — задача, которая на протяжении столетий увлекала математиков, любителей головоломок и решателей задач.

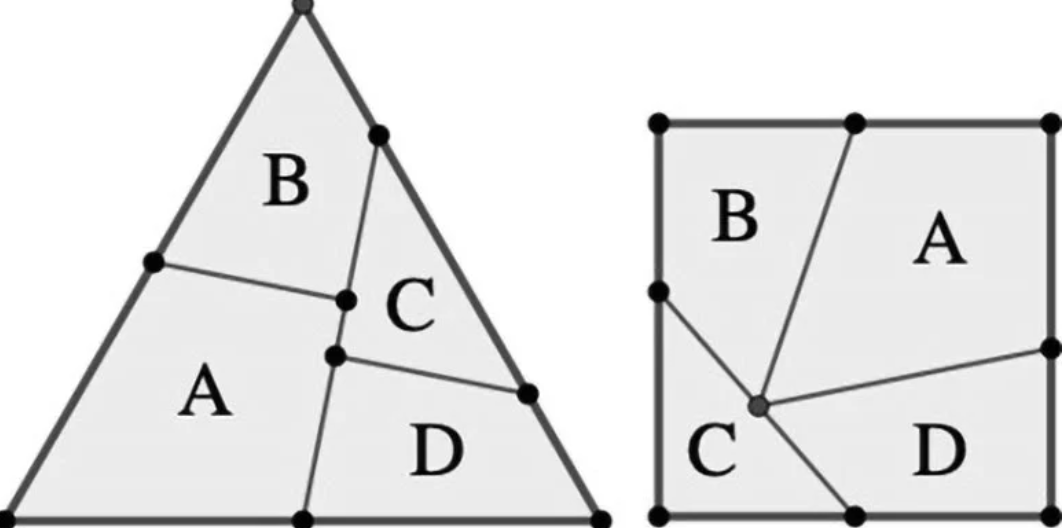
Головоломка Дьюдени остается одним из самых известных примеров геометрического рассечения. Помимо своей привлекательности для математиков, задачи рассечения имеют практическое применение в таких областях, как текстильный дизайн, инженерия и производство. Спустя более 120 лет после решения Дьюдени остается один вопрос: возможно ли решить головоломку с менее чем четырьмя частями?

В новаторском исследовании профессор Рюхей Уэхара и доцент Тонан Камата из Японского передового института науки и технологий (JAIST) вместе с профессором Эриком Д. Демейном из Массачусетского технологического института наконец ответили на этот вопрос. Они доказали, что первоначальное решение Дьюдени было оптимальным.

«Более века спустя мы наконец решили головоломку Дьюдени, доказав, что равносторонний треугольник и квадрат не имеют общего разреза с тремя или менее многоугольными частями, — говорит профессор Уэхара. — Мы достигли этого, используя новый метод доказательства, который использует диаграммы соответствия».

В своем исследовании ученые доказали ключевую теорему: не существует разреза между равносторонним треугольником и квадратом с тремя или менее частями, когда части запрещено переворачивать. Первоначальное решение Дьюдени также не включало переворачивание. Чтобы установить это, ученые сначала исключили возможность разреза на две части, проанализировав геометрические ограничения задачи.

Затем они систематически исследовали возможность трехчастного разрезания. Используя фундаментальные свойства разрезания, они сузили возможные комбинации методов разрезания для трехчастного разрезания. Наконец, они использовали концепцию диаграммы соответствия, чтобы строго доказать, что ни одна из этих комбинаций для трехчастного разрезания невозможна, тем самым доказав, что разрезание между квадратом и равносторонним треугольником не может быть достигнуто с тремя или менее частями.

Диаграмма соответствия сыграла центральную роль в их доказательстве. В этом методе набор разрезаемых частей, используемых при разрезании, сводится к структуре графа, которая фиксирует связь между ребрами и вершинами частей, образуя как треугольник, так и квадрат. Исследователи обнаружили, что этот метод применим не только к головоломке Дьюдени, но и может быть применен в целом к ​​другим задачам разрезания.

«Проблема разрезания и перестановки форм, как говорят, существует с тех пор, как люди начали обрабатывать шкуры животных для изготовления одежды. Такие проблемы также встречаются в любой ситуации, где используются тонкие материалы, — объясняет профессор Уэхара. — Наше доказательство открывает новые горизонты для понимания и решения проблем препарирования».

Хотя многие проблемы с рассечением были решены путем поиска решений с определенным количеством частей, никогда не было формального доказательства, показывающего, что определенное решение является оптимальным, используя наименьшее возможное количество частей. Метод, разработанный в этом исследовании, является первым, доказывающим такую ​​оптимальность.

«Наша методика показывает, что оптимальное рассечение возможно для реальных задач разрезания и перестановки. При дальнейшем уточнении она также может привести к открытию совершенно новых решений для задач рассечения», — заключает профессор Уэхара.

До этого ученые разгадали загадку кота Шредингера. На самом деле наша планета в мультивселенной. В 1935 году австрийский физик Эрвин Шредингер описал мысленный эксперимент, который выявил проблему в основе квантовой механики. Ее суть сводится к представлению о коте, существующем в состоянии неопределенности между жизнью и смертью. Физики-теоретики из Автономного университета Барселоны в Испании объяснили, почему кот Шредингера всегда находится в одном и том же состоянии.